In questi giorni si sono diffusi molti contenuti relativi al virus: dal basso, dall’alto, orizzontalmente. Io vorrei appuntare qui alcuni pensieri: una parte perlopiù impersonale sulle grandezze numeriche, la non linearità, l’eterogenesi dei fini e delle cause (espressione impropria che nel seguito rifiniremo) e su come sarebbe meglio discuterne; una parte sul rapporto fra noi e gli altri, in conseguenza di quanto sopra. In effetti il virus c’è solo come esempio, pur lampante e modello nel senso tangibile. Potrei fare una piccola selezione per segnalare almeno alcuni temi e punti di vista interessanti.
Il blogger e divulgatore matematico 3blue1brown ha prodotto un video per spiegare la natura esponenziale della crescita dei contagi a partire da concetti semplici: media di persone incontrate, probabilità di contagiarsi, un minimo di separazione/segregazione delle società [Exponential Growth and Epidemics].
Il Washington Post ha fornito delle simulazioni analoghe, per mostrare come frequenza e ampiezza dei movimenti e degli incontri influiscano sulla velocità di contagio e sul numero massimo di malati/ricoverati/immunizzati in un dato istante.
Esiste un sempre più famoso volume, Spillover di David Quammen (edito da Adelphi), e molti articoli e saggi come quelli del biologo socialista Robert G. Wallace, che raccontano invece da dove arrivino questi nuovi virus e la natura ecologica, agricola, produttiva, urbanistica di altre minacce infettive alla popolazione umana mondiale
Ci sono diversi post su come il virus sia una sorta di colorante prima e di reagente alterante poi, una sostanza che permette di visualizzare i flussi e i moti meccanici che tengono in piedi la “normalità”, e ci costringe a modificarli. Infine si trovano molti diari del lavoro, della quarantena, della sua psicologia, accanto ai flash-mob e le iniziative più semplici e dirette. Un passo di lato.
Nel mondo dei numeri
Ci si può adattare ad un ambiente mutevole e a sua volta adattabile, alcuni sistemi sono in equilibri stabili o instabili. Ci sono circa 7,8 miliardi di persone al mondo. Ci sono circa 60,5 milioni di persone in Italia. Questa seconda cifra è meno di un centesimo della prima. Le epidemie sono caratterizzate da fasi di crescita esponenziale. Le frasi qui sopra sono formalmente corrette e sembrerebbero corrette anche nei contenuti (le ho scritte in piena fiducia), forse sono vaghe e non si coglie il nesso, forse invece si può intuire.
Il punto, però, è che i concetti matematici dietro tali parole sono raramente compresi e introiettati, anche quando usiamo esplicitamente simboli e formule matematiche. Addirittura il funzionamento intimo e biologico della nostra percezione ha molto a che vedere con non linearità, fenomeni multi-scala e via dicendo, ma la nostra razionalità sembra fin troppo abituata o confinata ad approssimazioni lineari e monodimensionali.
Il primo nodo che vorrei presentare è quello degli ordini di grandezza e delle frazioni, in particolare percentuali. Il concetto è semplice ma genera complicazioni reali. L’ordine di grandezza di una quantità è la classe di grandezza, in un sistema in cui ogni classe è in un rapporto definito con la precedente. Familiarmente, in rapporto 10: unità, decine, centinaia, etc. e a ritroso decimi, centesimi, etc.
La tensione tra relativi e assoluti, frazioni e ordini di grandezza, si vede facilmente: 2 è quasi 3, c’è solo 1 di differenza; 2 è quasi il 66,67% di 3. Ebbene, 200 è quasi il 66,67% di 300, ma i numeri rapportati e la loro differenza sono cresciuti di due ordini di grandezza. Nulla di straordinario finché rimaniamo in astratto, ma i nostri interessi concreti su rapporti e differenze possono diventare facilmente inconciliabili.
Insomma, non tutti i 2/3 sono uguali, e questo perché spesso le funzioni (e in senso matematico, e pratico) dei numeri che maneggiamo non sono lineari come le proporzioni, e le regole locali approssimate non valgono globalmente. Emblemi della supposta razionalità e della sua rottura si trovano nel quadrato, nella sua diagonale, nel teorema di Pitagora. Esso assicura la costruzione di due quadrati le cui aree sono una doppia dell’altra.
Il rapporto tra i lati, che è lo stesso fra lato e diagonale del quadrato minore, è invece indefinibile “razionalmente”, cioè come frazione di due numeri naturali. Noi chiamiamo questo numero √2 “radice quadrata di due” e attorno alla sua irrazionalità e realtà si apre la potenza dell’infinito continuo, che destabilizzò a millenni di distanza i pitagorici, così come Georg Cantor. Dei primi, Ippaso, allievo più illustre, attorno al 500 a.C. sarebbe stato affogato per la scoperta o la divulgazione della prova che 1 e √2 sono incommensurabili. Il secondo dimostrò che questi numeri sono un’infinità più grande, diversa rispetto ai numeri razionali.
Morì impoverito in un ospedale psichiatrico nel 1918, dopo anni di critiche e riconoscimenti insufficienti. Rimanendo però nella finitezza, c’è un’altra lezione in questo esempio, ossia che i rapporti in una dimensione non si trasmettono banalmente in più dimensioni, dal lato all’area, oppure al volume.
Questo può deludere le nostre attese. Si impara a scuola e si ripete nei cicli formativi, ma proviamo a visualizzarlo: un millimetro, prendine mille e hai un metro. Un millimetro cubo, prendine mille e hai un… centimetro cubo. Prendine mille di questi e hai un decimetro cubo, cioè un litro. Ce ne vogliono mille a loro volta per riempire d’acqua un cubo di 1x1x1 m3, che non sembra enorme, potrebbe essere l’ingombro della postazione in cui state leggendo, e però peserebbe 1000 kg dopo il travaso. Il connubio di grandezze intensive ed estensive crea ulteriori paradossi.
A questo punto è interessante citare il Problema di Delo. Si narra che a Delo, città isolana sotto l’egemonia ateniese e devota al culto apollineo dai tempi micenei, imperversasse una peste. Gli abitanti consultarono dunque l’oracolo di Apollo, padre delle arti mediche e delle pestilenze, dio delle profezie e dei lumi intellettuali. La volontà divina fu chiarita: l’altare cubico dedicato al dio doveva essere raddoppiato in volume. Le maestranze si misero al lavoro e costruirono un altare il cui lato era il doppio del precedente, risultando in un cubo 8 volte più ingombrante. Ciò che raddoppiò fu quindi la furia pestilenziale del divino Apollo.

Figura 1 Un cubo di lato 1 e volume unitario, e il cubo di volume doppio: il suo lato è radice cubica di 2, circa 1.26
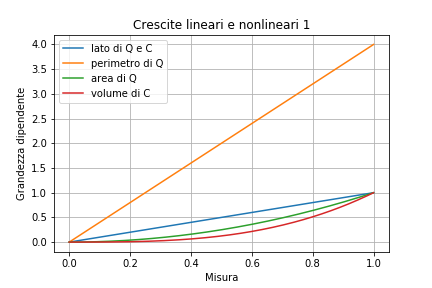
Così, il volume di un cubo in funzione del lato cresce in maniera non lineare, come già l’area del quadrato. La linearità è quella delle tabelline (sì, tutte), partiamo dal 2. Ad ogni passo (1, 2, 3, …), raddoppia il numero corrispondente: 2, 4, 6, … f(x) = 2x. Se invece ogni passo fosse la misura di un lato, e vi facessimo corrispondere l’area del suo quadrato Q, avremmo: 1^2, 2^2=4, 3^2=9, … g(x) = x^2. Al primo passo corrisponde un valore minore rispetto alla sequenza precedente, poi identico, poi superiore, e sempre di più. Nel piano cartesiano, disegneremmo una parabola che supera una linea e si dirige “più velocemente” verso l’infinito. Se nell’esempio precedente il valore della funzione fosse il volume del cubo C, avremmo: 1^3, 2^3=8, 3^3=27, … g(x) = x^3.
Una velocità e un’accelerazione ancora maggiori. Queste tre sequenze e curve crescono diversamente, nel primo caso ogni valore della funzione è superiore di due unità, ma via via la crescita percentuale si fa irrisoria. Certo, basta già questo ad andare verso l’infinito. Nel secondo e nel terzo caso la crescita assoluta è sia più veloce sia accelerata, ma ancora il tasso di crescita percentuale si riduce. Nella sequenza di cubi 1, 8, 27, 64, i rapporti fra un numero e il precedente sono 8, 27/8 e 64/27. Al millesimo passo il rapporto è quasi 1 (la differenza è però nell’ordine dei milioni…).
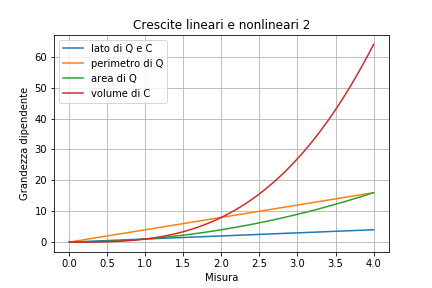
Ebbene, esiste una famiglia di curve caratterizzata proprio dall’avere un tasso di crescita costante, e in diversi contesti siamo abituati a sentire proprio di tassi di crescita come se potessero almeno teoricamente essere sempre costanti, senza pensare né agli assunti né alle implicazioni di una realtà che seguisse questa idea, o di una realtà che smettesse (comprensibilmente) di farlo.
Basti pensare al PIL, agli interessi sui debiti, e simili. Soffermiamoci allora sulla famiglia delle curve esponenziali. Nelle sequenze di quadrati e cubi c’è un esponente sempre uguale, 2 e 3. La loro famiglia è f(x) = x^a, con a fissato e maggiore di 1 che aiuta f(x) a crescere molto più velocemente di x.
Ma le funzioni esponenziali del tipo h(x) = a^x le superano sempre, essendo l’esponente a cambiare. Avere un tasso di crescita costante non significa avere una velocità costante, o un’accelerazione costante. Significa che anche la velocità e l’accelerazione crescono esponenzialmente. È come se ad ogni passo la sequenza h(x) saltasse di grado, copiando via via esempi più veloci dalla famiglia f(x): prima cresco come il lato del quadrato, al successivo aumento del lato già cresco come l’area, subito dopo come il cubo, poi l’ipercubo…
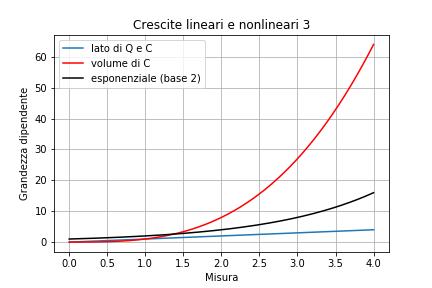

Se questo non dà immediatamente le vertigini, è perché, come la mente umana, la curva esponenziale ci mette un po’ ad ingranare. Ma esiste sempre una fase dopo la quale il percorso passato non ha più importanza, e qualunque confronto con curve lineari (o paraboliche, o cubiche…) diviene inconcepibile. Abbiamo visto quanto siano ingannevoli le percentuali, date qui come tassi costanti di crescita, o allo scorrere degli ordini di grandezza. Un altro modo per distinguere le curve esponenziali è proprio la misura dell’intervallo di tempo in cui i valori cambiano ordine di grandezza, è l’unico modo per tenere il loro passo. Ciascuna curva esponenziale ha un tempo o passo caratteristico di raddoppio, e analogamente di decuplicazione, e così via. Così se una grandezza aumenta esponenzialmente, ad esempio raddoppiando in un giorno, e un lunedì passa solo da 1 a 2, il lunedì successivo passerà da 128 a 256, e il terzo lunedì sarà ormai a 32 768. Desiderabile e raro con i soldi, sciagurato e plausibile per i contagi di una pestilenza.
Verso la realtà
Gli enti e le relazioni del mondo fisico sembrano spesso descritti molto bene da formule e relazioni matematiche, stranamente bene secondo certi fisici, tanto che si potrebbe argomentare che la matematica non descriva ma prescriva il comportamento di alcuni sistemi.
In altri casi la separazione è più evidente, ci sono misure macroscopiche il cui andamento tende ad una particolare curva matematica, e le misure relative a sottosistemi e sottostrutture hanno statistiche che si possono usare come parametri per costruire tale curva.
Ci sono poi casi in cui l’analogo matematico è troppo complicato per essere utile momentaneamente. Le nostre società si possono modellizzare come reti di persone o altri elementi, punti connessi da linee. I sistemi fisici (e non) sono trattabili spesso come enti con input, stato interno e output, con alcune funzioni evidenti e altre segrete che trasmettono e trasformano variabili note e ignote, di stadio in stadio.
Sovente abbiamo accesso e potere su parti degli input, siamo interessati a diverse parti dell’output, e l’ingegno deve ottenere il meglio dalla circostanza. Il mondo è una giungla di situazioni lineari e non, ordini di grandezza paragonabili e non, disaccoppiamenti, rapporti tra volumi e superfici che si capovolgono completamente affinché le forme rimangano uguali e semplici, mentre altre diventano complesse e frattali.
Non possiamo essere cognitivamente pronti a tutto, ma nonostante tabelline, conversioni metriche e studi di derivata, non usciamo neppure intellettualmente pronti dalle scuole. Nel frattempo, volenti o nolenti, coscienti o no, ci ritroviamo a partecipare della complessità del mondo, ad accrescerla, persino mentre cerchiamo di indagarla o controllarla. O quantomeno dipendiamo, anche nelle nostre attività minori, da processi di questo genere ai quali partecipano altri esseri umani per noi.
Recuperiamo l’esempio iniziale, 7.8mld di abitanti nel globo e 60.5mln di abitanti in Italia, 2 ordini di grandezza tra loro, una differenza quasi identica al primo numero. Eppure, all’interno vi sono innumerevoli strutture e relazioni non ancora espresse da questi conti.
Nella realtà non si trovano curve di crescita perennemente esponenziali. Ci sono fasi che vengono interrotte dai limiti interni ed esterni dei sistemi fisici, risorse di spazio o energia ad esempio, saturazioni. Quelle che sui grafici sono curve e magari punti di flessione, cambiamento radicale, corrispondono ad eventi fisici drammatici (a volte solo nel senso originale relativo all’azione, a volte anche nell’accezione più luttuosa).
In una ricerca parzialmente ironica, il fisico Heinz von Foerster presentò la Doomsday Equation. Secondo i suoi dati la crescita della popolazione umana era più che esponenziale.
La curva esponenziale, come visto, ci sfugge facilmente d’occhio e di mano, perché una misura raddoppia ogni “periodo” fisso. Stando ai dati di von Foerster la popolazione mondiale aveva un periodo di raddoppio decrescente (!), ed essendo al 1960 sui 2.7 miliardi, la sua crescita sarebbe diventata infinita per il 2026, esattamente al 13 novembre, 115esimo compleanno del fisico.
Ovviamente esistono numerosi limiti, da quelli fisici a quelli sociali, per cui la cosa non si possa realizzare, e allo stesso tempo è interessante indagare le retroazioni positive, quell’eterogenesi dei fini che permette al fenomeno di sussistere e seguire per diversi secoli un’equazione impossibile in eterno.
Ad esempio, con la popolazione aumentano (linearmente?) gli individui innovatori tecnologici, le cui scoperte favoriscono direttamente la vita e la riproduzione, aumentando la quantità di risorse disponibili o l’efficienza del loro uso per il sostentamento, ad esempio.
A tal riguardo comunque non si stia ingenuamente sereni, con Al Bartlett, altro fisico nato nel secolo scorso ed evangelizzatore sul tema. Per lui, la mancata comprensione della curva esponenziale sarebbe il maggior difetto della nostra specie o società. Si noti innanzitutto che è carente parlare di sostenibilità o sovrappopolazione solo contando gli esseri umani, senza considerare chi produce o consuma cosa, come e perché, a maggior ragione date le ipotesi su ciò fino ad oggi abbia sostenuto la demografia “ultra-esponenziale” dell’umanità; e poi si citi comunque la parabola di Bartlett sui batteri in bottiglia. Immaginiamo di mettere un batterio il cui periodo di riproduzione, e cioè duplicazione, sia 1 minuto.
Lo introduciamo nella bottiglia (a risorse ignote ma finite) alle 11, e alle 12 notiamo che la bottiglia è colma e la colonia spacciata. Bene, per la stragrande maggioranza del tempo la bottiglia è stata più che vivibile e la dinamica non è mai cambiata: fino alle 11:59 metà era ancora tutta da colonizzare. Bartlett chiede se foste batteri, quando iniziereste a preoccuparvi? Per una quantità che raddoppia ogni “periodo” ma ha un limite esterno, il “giorno” prima dell’apocalisse il limite sembra ancora distante e irraggiungibile in tempi storici; in alcuni casi acceleriamo verso un muro che, benché invisibile, è già entro lo spazio di frenata disponibile. A volte possiamo controllare il muro, a volte il veicolo, entrambi o nessuno. Se vi viene in mente il cambiamento climatico, le influenze e le risposte antropiche, il futuro delle nostre risorse, allora pensiamo in maniera simile. Ma la metafora sta diventando ancora più saliente dal punto di vista epidemiologico. Le epidemie hanno solitamente una curva del numero di contagiati nel tempo che segue un andamento crescente esponenziale, in una popolazione.
Non all’infinito, ovviamente, ma dietro alla flessione ci sono diversi fenomeni, neutri (una popolazione è finita), positivi (come l’immunizzazione), negativi (come la morte, ammesso che effettivamente blocchi la contagiosità). Caratteristiche naturali, ambientali e non solo, tanto del virus quanto della popolazione (specie, rete o struttura sociale in cui esso si diffonde), determinano la stima dei parametri dell’esponenziale che meglio descriverà il fenomeno, nel bagaglio di tutte le curve possibili. La tendenza al comportamento esponenziale suggerisce come ogni azione di contrasto debba essere veloce e precoce, per avere efficacia.
La relazione tra i fenomeni concreti e le stime matematiche invece ci impone particolari problemi di controllo, poiché non abbiamo accesso diretto a parametri puramente matematici, e spesso nemmeno alle variabili e alle strutture fisiche e organizzative da cui quelli derivano. Per una indagine approfondita dei provvedimenti politico-sociali possibili e dei loro effetti in base alla bontà di esecuzione, si veda il report 9 dell’Imperial College London. In tutto ciò, è da determinare quali siano gli obiettivi di una popolazione o del suo governo, e le “funzioni di valore” attribuite ai numeri.
La Storia, biologica prima che umana, è caratterizzata dal problema del controllo in senso cibernetico e quindi dalla eterogenesi dei fini. Il filosofo e fondatore della psicologia Wilhelm Wundt ha coniato (1886) tale espressione per evidenziare come perseguire un fine produca necessariamente effetti indesiderati, che possono però diventare fini a loro volta. Ma viviamo anche una sorta di esperienza dell’eterogenesi delle cause: abbiamo la problematica dell’interpretazione delle azioni e dei fenomeni individuali o collettivi, intenzionali o no, nelle possibili combinazioni.
Vi sono sistemi le cui parti, con azioni semplici, danno luogo ad un comportamento collettivo complesso, persino finalistico, così come vi sono sistemi in cui elementi complessi e profondi, come lo è una persona, si sommano in una produzione più semplice, più miope, inerte. Ed altre varietà ancora. Questo campo concettuale ha in realtà una tradizione che può risalire a Niccolò Machiavelli e Giambattista Vico, fino a Norbert Wiener e oltre. Tornando dunque ad un esempio, umano e storico, prendiamo la Cina pre-epidemica e la numerosità della popolazione.
Negli anni ’60 i vertici del Partito iniziarono a preoccuparsi del boom di nascite, con le sue cause pregresse e le sue potenziali conseguenze, ad esempio in termini di risorse, per come venivano prodotte e consumate all’epoca. In Cina un quarto della popolazione mondiale aveva a disposizione meno di un decimo della superficie coltivabile, ad esempio. Nel 1979 sotto Deng Xiaoping, accanto alle riforme economiche, venne varato un regime legislativo di controllo biologico, la politica del figlio unico.
La popolazione è qui un sistema dinamico, la cui numerosità futura è l’output di interesse. Una popolazione grande banalmente cresce di molte unità anche se il tasso di fertilità è basso, e agire su questo non poteva che avere un effetto desiderato ritardato.
Nel mentre ne sono scaturiti altri, come l’invecchiamento della popolazione, la riduzione della percentuale attiva e affini, mentre i consumi medi, la produzione e l’efficienza per sostenere la popolazione sono cambiati. Ad oggi, le sanzioni pecuniarie partono con il terzo figlio (e c’è chi può permettersi di affrontarle).
Dentro il presente, dentro il futuro
È giunto il momento di citare direttamente il nuovo coronavirus, il SARS-CoV-2, da cui la sindrome covid-19. Quanto alle percentuali e le dimensioni dei fenomeni, ricorderò questo: al 19 marzo*** in Italia i casi totali riconosciuti di persone infettate (già guarite, già morte e correntemente positive) sono 41 035. Solo lo 0.0678% della popolazione.
Insomma, se non conoscete direttamente nessun infetto c’è un motivo non complottistico, ancora una volta siamo nel meno di un millesimo. Eppure si può ipotizzare che fino al 75% della popolazione infetta non sviluppi alcun sintomo, e in questo ragionamento la stima è pessimistica, ma in un altro contesto sarebbe ottimistica, nel senso che solo il 25% dei casi di contagio sarebbe di qualche disturbo all’infetto.
Prendendo quindi tale stima “pessimistica” e rincarando con l’ipotesi che le misure restrittive dei governi non siano minimamente efficaci (laddove l’efficacia è la vicinanza al risultato sperato, ridurre il contagio, mentre l’efficienza è la convenienza del costo per ottenerlo), potremmo stimare circa 160mila infetti al 19 marzo, senza preoccuparci della non contagiosità dei defunti nel periodo, di immunizzazioni o “guarigioni” dalla positività asintomatica, solo quadruplicando i casi totali ufficiali (25% della stima pessimistica).
Saremmo ora a poco più che due millesimi della popolazione italiana.
Questi calcoli però sono puramente ludici e inaffidabili, per i coefficienti stimati nonché per la correttezza dei dati in sé [invito alla nota per aggiornamenti e nuove stime]; l’ordine di grandezza apre comunque a due linee di riflessione, almeno.
1. Il rischio personale di essere ora degli infetti è ancora relativamente basso nell’ottica nazionale, invero simile a quello generalizzato di morire di influenza stagionale, avendola presa. Ciò potrebbe essere impropriamente letto come se la quasi totalità della popolazione, sempre di 60 e più milioni, non fosse a rischio immediato di ammalarsi, né di diffondere il virus – men che meno andando a correre -, eppure la totalità vive a tutti gli effetti in un regime restrittivo con varie conseguenze (però disuniformi, com’è disuniforme la pericolosità del virus) che esulano dall’epidemia, ma non necessariamente dalla salute pubblica (suicidi, TSO, violenze domestiche, …). Ma in realtà si è già detto che una popolazione è organizzata e si muove in strutture latenti, in reti di contatti. Inoltre, il fenomeno ha diverse scale su cui esaminarne lo stato, modificarlo.
Dunque non si può considerare la probabilità di entrare in contatto con un infetto, e quella dipendente di essere contagiati, come una semplice estrazione casuale da un parco uniforme, una lotteria classica. Se non conoscete ancora nessun infetto, è comunque probabile che ne conoscano i vostri contatti, e che non siate a molti gradi di separazione da qualcuno venuto a mancare. Esistono edifici ad alta carica virale (i posti di lavoro ancora aperti, gli ospedali), cluster familiari e di affetti, focolai provinciali, regioni colpite diversamente e sottoposte a varie misure reattive durante fasi diverse del contagio.
Ci sono esempi in cui la strategia applicata è stata “sudcoreana” (tampone ad asintomatici, tracciamento, quarantena a bersaglio, come a Vo’ Euganeo), “cinese” (quarantena generalizzata, idealmente nella zona rossa lodigiana e poi nazionalmente), “lombarda” (quarantena ma greve lassismo sulla mobilità e la sicurezza nel lavoro, tamponi insufficienti, fra Milano, Bergamo e Brescia).
Tutto ciò nello spazio di poche province addirittura confinanti.
2. Allo stesso tempo il Sistema Sanitario Nazionale e le sue implementazioni regionali sono già sotto uno stress enorme: apparentemente nessuna popolazione di ordine di grandezza superiore alle decine può permettersi un numero di posti letto ospedalieri, men che meno da terapia intensiva, e una quota di personale sanitario del suo stesso ordine di grandezza.
Al di là dei – comunque pessimi – tagli alla sanità pubblica, una situazione che richieda il ricovero di millesimi da una popolazione plurimilionaria è assolutamente critica: migliaia di morti sono sempre migliaia di morti, che siano contati da un bacino di decine di migliaia per calcolare la letalità del virus (numero di morti su numero di malati), o che siano contati fra i milioni o miliardi delle popolazioni nazionali o mondiale per calcolare la mortalità della pandemia (numero di morti sulla popolazione generale).
“Appiattire la curva” serve ad evitare un tracollo ulteriore, e questo è un concetto non scontato che pare essere stato colto dal pubblico inizialmente ignaro. Forse si può sostenere e argomentare, ma sarebbe probabilmente inutile, che sia davvero meno violenta la frase (falsa) “tanto muoiono solo gli anziani già malati” rispetto a “tanto muoiono solo lo zero-virgola… della popolazione”.
Fatto sta che la realtà si manifesta alla nostra mente con quella che davvero è una contraddizione, come piace dire ai filosofi sociali: lo stesso fenomeno è in un aspetto un rischio medio individuale piccolo e monodimensionale (e già la media è notoriamente ingannevole), in un altro un rischio sistemico tangibile e di conseguenze multivariate ed enormi, nonché un attacco a valori astratti.
La maggior parte dei media, dei decisori, e forse persino alcuni tecnici non si sono dimostrati né pronti né capaci di adattarsi a dinamiche che saremmo ipocriti a definire “unknown unknowns”. Dove possibile bisogna contribuire all’affinamento delle risposte, comprendere anche la possibilità di errore.
Contemporaneamente però è necessario vigilare, discutere e ricordare espressioni e azioni dei soggetti principali, insieme alla situazione dei tanti e degli ultimi.
Non siamo cognitivamente predisposti ad affrontare fenomeni di dimensioni multiple e dinamiche esponenziali, problemi di controllo, percentuali su ordini di grandezza distanti dalla percezione sensoriale quotidiana; ma possiamo e dobbiamo prepararci intellettualmente. Innalziamo il nuovo altare di Apollo.
***Al 24 marzo, ore 18:00, abbiamo nuovi dati e stime sull’entità dei casi positivi non testati, asintomatici o sintomatici. Le persone attualmente positive per la Protezione Civile sono 54 030 (quasi un millesimo della popolazione), con 69 176 casi totali. Per il virologo Andrea Crisanti potrebbero esserci fino a 450 mila casi di infezione (si andrebbe verso un centesimo della popolazione, 8-10 volte maggiore delle conferme ufficiali, e sarebbe un dato inquietante).
Visioni e letture d’interesse:
Blog post di 3blue1brown https://www.3blue1brown.com/videos-blog/exponential-growth-and-epidemics/
Washington Post, “simulitis” https://www.washingtonpost.com/graphics/2020/world/corona-simulator/
ICL report 9 https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/news–wuhan-coronavirus/
Intervista al dottor Ernesto Burgio https://www.ondarossa.info/redazionali/2020/03/coronavirus-origini-effetti-e?fbclid=IwAR0p_mWzi7gqeTldbbmITJnCX1K9uJzs3Jo4hM_pRF_oeB46d5taKlZFVn8/
Robert G. Wallace agli inizi dell’epidemia https://www.counterpunch.org/2020/02/24/connecting-the-coronavirus-to-agriculture/
Dottor Giuseppe Imbalzano sugli errori della Regione Lombardia https://www.sanitainformazione.it/salute/coronavirus-imbalzano-ospedali-misti-e-malati-trasferiti-due-errori-che-dovevano-essere-evitati/
Andrea Crisanti sugli errori delle rilevazioni e stime https://www.corriere.it/cronache/20_marzo_24/coronavirus-crisanti-emergenza-sottovalutata-italia-450-mila-casi-questo-fallimento-ee6b83fc-6e0c-11ea-9b88-27b94f5268fe.shtml
Gullo, E. (2020) Un tentativo di epistemologia politica su #Covid-19. in Blog Studi Sulla Questione Criminale [online]. Disponibile al seguente link: https://wordpress.com/post/studiquestionecriminale.wordpress.com/2266
(Vorrei ringraziare in primis Laura Tripaldi, poi Carlo Corradini, Margherita Ronchini, Francesco D’Isa e Lerio per alcuni appunti e dialoghi attorno alle questioni poste qui.)

